Untuk lebih memahami mengenai kesebangunan dan kekongruenan bangun datar, perhatikan beberapa contoh soal berikut. Contoh 1: Kesebangunan Dua Persegi Panjang
Psersegi panjang ABCD memiliki panjang dan lebar secara berturut-turut 13 cm dan 39 cm. Jika persegi panjang ABCD tersebut sebangun dengan persegi panjang KLMN, yang sisi terpanjangnya memiliki ukuran 24 cm, tentukan panjang sisi terpendek dari persegi panjang KLMN.
Pembahasan Persegi panjang ABCD dan KLMN dapat digambarkan sebagai berikut.

Karena persegi panjang ABCD sebangun dengan KLMN, maka panjang sisi-sisi yang bersesuaian dari kedua persegi panjang tersebut merupakan perbandingan yang senilai. Sehingga,

Jadi, panjang sisi terpendek dari persegi panjang KLMN adalah 8 cm.
Contoh 2: Kesebangunan pada Persegi Panjang
Perhatikan gambar di bawah ini!

Jika diketahui AB = 144 cm dan BC = 108 cm, persegi panjang ABCD, BCGF, dan EHGD merupakan persegi panjang-persegi panjang yang sebangun, tentukan luas daerah AFHE!
Pembahasan Karena persegi panjang ABCD sebangun dengan persegi panjang BCGF, maka
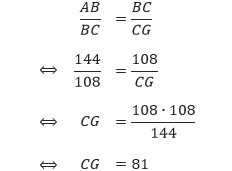
Karena CD = AB = 144 cm dan CG = 81 cm, maka EH = GD = CD – CG = 144 – 81 = 63 cm. Diketahui ABCD juga sebangun dengan EHGD, maka didapatkan

Sehingga, FH = FG – HG = BC – HG = 108 – 47,75 = 60,25 cm. Diperoleh luas dari segi empat AFHE adalah EH × FH = 63 × 60,25 = 3.795,75 cm².
Psersegi panjang ABCD memiliki panjang dan lebar secara berturut-turut 13 cm dan 39 cm. Jika persegi panjang ABCD tersebut sebangun dengan persegi panjang KLMN, yang sisi terpanjangnya memiliki ukuran 24 cm, tentukan panjang sisi terpendek dari persegi panjang KLMN.
Pembahasan Persegi panjang ABCD dan KLMN dapat digambarkan sebagai berikut.

Karena persegi panjang ABCD sebangun dengan KLMN, maka panjang sisi-sisi yang bersesuaian dari kedua persegi panjang tersebut merupakan perbandingan yang senilai. Sehingga,

Jadi, panjang sisi terpendek dari persegi panjang KLMN adalah 8 cm.
Contoh 2: Kesebangunan pada Persegi Panjang
Perhatikan gambar di bawah ini!

Jika diketahui AB = 144 cm dan BC = 108 cm, persegi panjang ABCD, BCGF, dan EHGD merupakan persegi panjang-persegi panjang yang sebangun, tentukan luas daerah AFHE!
Pembahasan Karena persegi panjang ABCD sebangun dengan persegi panjang BCGF, maka
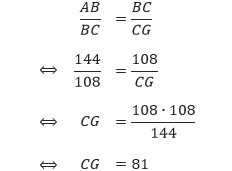
Karena CD = AB = 144 cm dan CG = 81 cm, maka EH = GD = CD – CG = 144 – 81 = 63 cm. Diketahui ABCD juga sebangun dengan EHGD, maka didapatkan

Sehingga, FH = FG – HG = BC – HG = 108 – 47,75 = 60,25 cm. Diperoleh luas dari segi empat AFHE adalah EH × FH = 63 × 60,25 = 3.795,75 cm².

