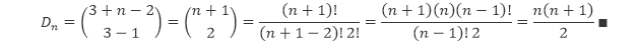Banyak sekali fakta-fakta menarik dalam segitiga Pascal. Setiap baris pada segitiga Pascal memuat bilangan-bilangan yang merupakan koefisien dari bentuk dari ekspansi pangkat bilangan cacah dari binomial, salah satunya. Akan tetapi, pada pembahasan ini akan dikhususkan untuk menemukan pola bilangan dalam setiap diagonal segitiga Pascal tersebut. Perhatikan gambar berikut.
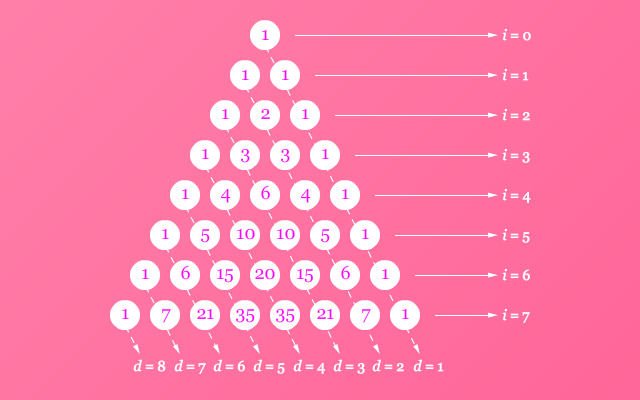
Untuk menemukan pola tersebut kita akan membutuhkan pola bilangan dalam setiap baris segitiga Pascal. Semua bilangan dalam setiap baris tersebut merupakan koefisien dari ekspansi pangkat dari binomial. Sebagai contoh,
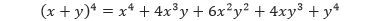
Koefisien dari ekspansi pangkat 4 binomial tersebut adalah 1, 4, 6, 4, dan 1 yang merupakan bilangan-bilangan pada baris ke-4 pada segitiga Pascal. Menurut Teorema Binomial,
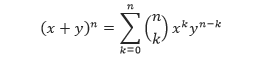
Sehingga secara umum barisan bilangan pada baris i = k dalam segitiga Pascal dapat dituliskan,
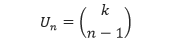
Sebagai contoh, bilangan ke-2 dan ke-3 dari baris ke-5 segitiga Pascal adalah,
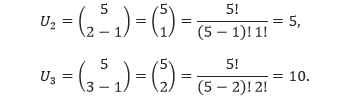
Berdasarkan pola di atas, kita dapat menurunkan rumus untuk menentukan bilangan ai,j, yaitu bilangan yang berada pada baris ke-i dan kolom ke-j dalam segitiga Pascal.
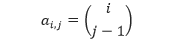
Misalnya, kita dapat menentukan bilangan yang berada pada baris ke-7 dan kolom ke-6 sebagai berikut.
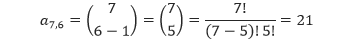
Dari rumus ai,j tersebut, kita dapat menuliskan barisan bilangan pada diagonal ke-d sebagai berikut.
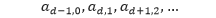
Atau dapat dituliskan sebagai,
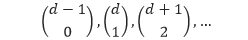
Sehingga, suku ke-n dari barisan bilangan pada diagonal ke-d adalah
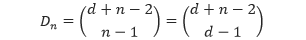
Sebagai contoh, pada diagonal ke-3 segitiga Pascal merupakan bilangan-bilangan segitiga yang memiliki pola n(n + 1)/2. Barisan ini akan kita uji dengan menggunakan rumus yang baru saja kita temukan. Dengan d = 3,